Preface: Before 2012 once again embroils us fully into the ongoing saga of the eurozone’s Crisis and its global ramifications, I thought it might be a good idea to start the year on a reflective mood. The topic I chose is complexity and the inadequate responses to it that have landed us in a mire of our own making; a Crisis that could have been defeated during 2011, and that it is still possible to stop on its tracks in 2012. Yet a Crisis which will probably be allowed to run its terrible course, with hideous consequences for Europe and the world, as a result of a motivated flight from rational responses to a complex, yet not insoluble, problem.
Introduction: Complexity is the stuff of existence and its proper acknowledgment a prerequisite for a successful life. Our problematic relation with complexity has been a cause of many a calamity, the Crash of 2008 and its aftermath (especially here in the eurozone) being a case in point.
Wherever we look, and the Earth’s environment is not a bad place to start, humanity has struggled to come to terms with complex systems. Economies, the archetypal human artifact, are even more notorious than ecologies for evolving in ways that humans cannot grasp by means of our run-of-the-mill, pacifying, oversimplifying models. And when our actions, policies and choices, based as they tend to be on such models, give rise to meltdowns, crises and stubborn failures, we have a tendency to move to the other extreme; the one I like to label Complexity Fetishism’. It seems to me that the great challenge for 2012 is to find ways of plotting a course that avoids the pitfalls of both Complexity Denial and Complexity Fetishism.
This four-part series of posts will comprise the following installments.
Part A: The analytic-synthetic approach to socio-economic systems as a form of Complexity Denial
Part B: The political lure of naive models in the era of financialisation
Part C: Crisis and the temptation of Complexity Fetishism: The eurozone case
Part D: A challenge for 2012: How to transcend the sterile confrontation of Hayekians, Keynesians and Marxists
Today we begin with Part A. Parts B,C and D will be added in regular intervals within January.
Part A – The analytic-synthetic approach to socio-economic systems as a form of Complexity Denial
A.1 The lure of the ‘analytic-synthetic’ approach: The bewildered watchmakers
Consider the analytic-synthetic method of a watchmaker faced with a strange mechanical watch. First, she takes it carefully apart with a view to examining the properties and function of each of its tiny cogs and wheels. Then, she screws it back together. If a reassuring ticking sound ensues, this must surely mean that the fragments of knowledge imparted by the separate study of each of its parts were successfully synthesised into a macro-theory of the watch.
This parable of an ideal reductionist, analytic-synthetic economic approach has been implicit to economic theorising since the first stirrings of what today counts as economics-proper; the sort of economics practised and taught in the world’s (i.e. US) best schools. To the economists who sought a break from the politically motivated, fully discursive ‘mumbo-jumbo’ of Adam Smith, David Ricardo, Karl Marx, but also of Ludwig von Mises, Joseph Schumpeter and Friedrich von Hayek, the analytic-synthetic approach (and a new focus on ‘rational economic man’) became the litmus test of ‘scientific’ economics (see Philip Mirowski’s, excellent 1989 book, Against Mechanism).
In this new ‘scientific’ mind frame, individuals are the equivalent of the watchmaker’s cogs and wheels: parts of a whole to be understood fully (complete with determinate behavioural models) and independently of the whole their actions help bring about. Thus, any socio-economic phenomenon under scrutiny is to be explained via a synthesis of partial knowledge derived at that individual level.
But there is a snag: Unlike the world of mechanical watches, society consists of ‘parts’ which lose their ‘properties’ once separated from one another. A pulley or a cog can be fully described in isolation to the other mechanical parts with which it was designed to work harmoniously. Indeed, the ‘relations’ between the watch’s parts are straightforwardly revealed, to the trained eye, through close inspection of the parts’ shape, size and other physical properties. In the social world, however, things are different. When Aristotle spoke of humans as political animals, or when Hegel narrated his master-slave paradox, they were dwelling on this radical difference between the constituents of society as opposed to the parts of mechanical systems (regardless of their complexity). More precisely, in society (as opposed to the internals of a watch) the relations between its ‘parts’ (i.e. people) are not deducible from primitive data concerning these ‘parts’ alone (e.g. from data on persons’ means and ends) but, also, it is simply impossible to understand the properties of ‘parts’ (or persons) in isolation to one another.
In summary, economists try to ‘analyse’ economic systems like watchmakers taking apart a mechanical watch. Yet, to their dismay, they soon realise that the various ‘parts’ lose their integrity the moment they are isolated from the ‘whole’ which they make up. But the lure of mechanism, of the analytic-synthetic approach, is too strong. It is an approach that promises economists the title of ‘scientist’ with all the perks that come with this identity. Thus, they persist with the watchmakers’ strategy. Alas, when they put the watch back together, once they have completed their study of its ‘parts’, they find that it does not work. That the only way they can claim success (i.e. understanding the social economy) is by faking their results; by presenting their clearly malfunctioning models as relevant. This they can get away with only if and when their audience is too blinded by the models’ mathematical complexity to notice that they fail miserably to account for the real complexity they are supposed to… model. The next section, A.2, offers a stylised example.
A.2 The revenge of irreducible complexity: Penny pinching yields pennies (even when riches are readily available)
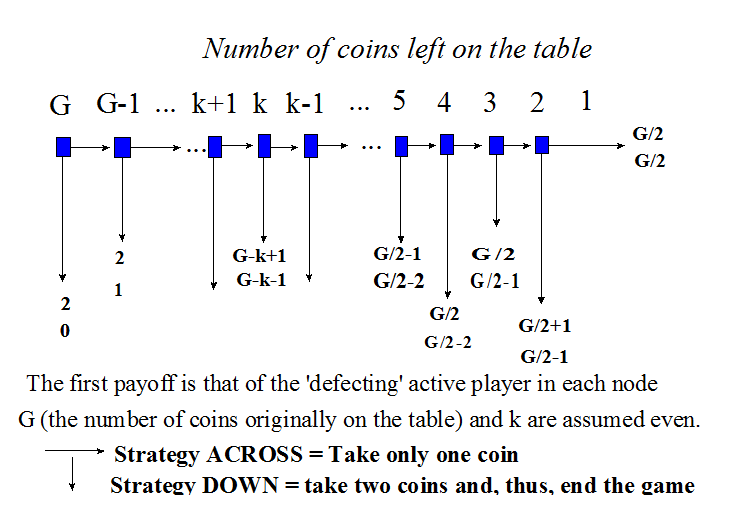
Imagine a table piled up with ten thousand gold sovereigns. Ann and Ben are given the opportunity to take them all as long as they respect a simple rule. They must approach the table one at a time and, on each approach, collect a single coin (with Ann kicking the process off). Crucially, they are also given the right to collect two coins on the understanding that, the moment either player exercises that right, the game ends with the remaining coins withdrawn. In short, if the person collecting at any visit takes two coins at once, it is ‘game over’ for both (though they can hold on to the coins they have already collected). To continue visiting the table, accumulating more and more coins until there are none left, neither must collect more than one coin at the same visit. As long as Ann and Ben collect a single coin every time they come to the table, they shall clean up (amassing five thousand gold sovereigns each). But will they?
The analytic-synthetic approach, when combined with greed, comes to a startling conclusion: If rational, and ‘analytic-synthetic’ in their thinking, Ann will end up with two coins while Ben will end up with nothing! Thus, a rational Ann is instructed to collect two coins on her first visit, thus ensuring that 9998 coins are wasted! But how can this be rational?
This is how the analytic-synthetic approach reaches its misanthropic conclusion: Assuming that Ann and Ben are rational people who try to work out analytically how to behave in this game, the analytic-synthetic approach (the watchmaker’s method) invites them to break the gaming process into its constituents ‘parts’, study each one separately, and only then put together the derived knowledge into an overall strategy for playing this game. The following figure offers a break-down of the overall game into its ‘parts’, so as to allow us to see how the analytic-synthetic reaches its paradoxical conclusion. [Note that the figure allows for the more general case of G coins, in our case G=10000, plus more than two players; here we stick to two: Ann and Ben.]
Like plotting a course out of a maze, it is easiest to do so by starting at the ‘end’ (in the maze’s case the ‘exit’, here the last visit at the table) and work backwards. Here is what Ann expects to happen in each stage, beginning with the last one first:
Last stage – 2 coins left on the table: Ben is visiting the table and will, obviously, take both coins.
Penultimate stage – 3 coins left on the table: At this stage it is Ann’s turn to visit the table. Should she take one or two coins? She will, of course, collect two of the remaining three coins as she is anticipating that, were she to take only one, the game will shift to the last stage (see above) where Ben will collect both remaining coins. Ann, naturally, prefers to be the one that collects the 2 out of the, currently, remaining 3 coins. [Note: One coin is ‘lost’ to both players].
Last stage but 3 – 4 coins left on the table: Ben is visiting the table, knowing (see above) that if he collects one coin, then Ann will end the game by collecting two. Thus, he chooses to collect 2 coins himself. [Note: Two coins are ‘lost’ to both players.]
…
Second stage – 9999 coins left on the table: Ben is at the table. For reasons already seen, he expects that if he takes one then Ann will take two. So, he takes 2 coins, so as not to be left with a single coin. [Note: 9997 coins are ‘lost’ to both players.]
First stage – 10000 coins on the table: Ann is kicking off the game. She has worked out (see immediately previous paragraph) that, given a chance, Ben will end the game immediately. So, she chooses to do the best she can for herself, under the grim circumstances: She collects two coins immediately, ending the game. [Note: 9998 coins are ‘lost’ to both players.]
Summary: It can be brilliantly rational to act irrationally
The analytic-synthetic approach to complex socio-economic interactions suggests that we break the latter down to their constituent ‘parts’ (stages of the game in the above example), study each one individually (just like the watchmaker studies a mechanical watch’s cogs and wheels) and then synthesise what we have learnt to come up with an overall conclusion about what it is best to do and how to behave ‘optimally’. In the example above, this method yields a paradoxical piece of advice: Waste 9998 of 10000 available gold sovereigns! Could this be good advice? Of course not.
So, where is the snag? The snag resides in the analytic-synthetic approach itself. It is simply untrue that the complexity caused by this strategic interaction can be reduced by breaking the overall interaction into smaller ‘parts’ that are then studied as separable interactions. Indeed, it is a grave error to think that we can reduce complexity via the analytic-synthetic approach in any complex interaction that involves strategic, inter-dependent, thinking of the sort that is prevalent everywhere – from party goers deciding what to wear at the party to the money markets. Why not? Because the
analytic-synthetic approach to interactions like the one in our coin example requires what philosophers refer to as fallacious ‘counterfactuals’.
Here is the main counterfactual involved: Did you notice that the whole analysis began at the last stages, or ‘parts’, of the interaction (at the point when there were only three coins left and Ann had to choose between collecting one or two coins)? And that, on the basis of that answer extracted from the last stages, the analysis told Ann to collect two coins at the very beginning (when all 10 thousand coins lay on the table)? In short, Ann was advised to end the game at the outset on the basis of an analysis of what would have happened if it continued to the end; i.e. if she… ignored its advice!
But if it is uniquely rational to collect two coins whenever one is given a chance to visit the table, how can we apply rational analysis to much later parts of the game that rational players would never reach (since, if rational, their behaviour would have killed the game off ages before)? This is the killer counterfactual that ought to lead us to the only safe conclusion here: There exists no uniquely rational way to play this game!
Yes, there is an analytic-synthetic logic that advises Ann to kill the game immediately. But there are compelling arguments that subvert the analytic-synthetic logic and point in precisely the opposite direction. Like the one which follows:
The logic of penny-pinching left Ann with pennies, Ben with nothing, and a whole lot of gold sovereigns lost to both. Awfully wasteful outcomes of this nature abound all around us: Smart people falling prey to their own ‘cunning’. And yet this type of failure is neither inevitable nor genuinely rational. It is just what we get when a most narrow sense of rationality takes over from reasonable judgement. Thankfully, a truly rational Ann can escape the straightjacket of the economists’ foolishness (parading as the utmost in rationality) as long as she is willing to think critically. Here is how:
Suppose that a rational Ann is, indeed, impressed by the analytic-synthetic logic and the wisdom of collecting 2 coins at the beginning. But suppose too that her critical thinking cannot rest until she asks her own ‘counterfactual’:
“What if I do not do as the analytic-synthetic method suggests? What if I collect only one coin? How will Ben respond? Is there no chance that he will think that I have gone bonkers, or soft-headed, or altruistic (i.e. caring not only about how many coins I get but also interested in his take too)? And if by taking a single coin now I give him a reason to take only one coin in the second stage, if only to give me another chance to ‘mess up’ (i.e. to collect a single rather than two coins) in the third stage, then why not do so? For if this ploy, of appearing ‘irrational’ or ‘altruistic’ to him, does the trick, then I get a chance to collect at least three coins (one now and two in stage three). What is so ‘irrational’ or ‘altruistic’ about that?”
The answer is “nothing”. Thus, following a good hunch, Ann realises that she can profitably subvert Ben’s expectations by diverging from the edicts of the economists’ logic. Indeed, she realises that such subversive behaviour increases not only her payout but also Ben’s. So, if it is rational to subvert the analytic-synthetic method, the latter cannot possibly maintain the monopoly on good advice or, indeed, good analysis. In fact, the analytic-synthetic approach proves analytically, and logically, flawed. In the end, the only thing that rational Ann can do is rely on a form of judgement that is irreducible to calculation.
As I wrote in the conclusion to the previous section, “economists try to ‘analyse’ economic systems like watchmakers taking apart a mechanical watch. Yet, to their dismay, they soon realise that the various ‘parts’ lose their integrity the moment they are isolated from the ‘whole’ which they make up.” In the gold sovereign game above, the point was that trying to isolate the game’s various stages from one another and, then, to synthesise those analyses into a grand theory of what Ann and Ben ought to do fails miserably because Ann and Ben are… cleverer than that; because rational humans can subvert the silly advice arrived at mechanistically by means of analytic-synthetic approaches suited well for algorithms (which cannot question their own programming) but wholly inappropriate for sentient humans who perfectly able to subvert the rules that ‘ought’ to be governing their behaviour.
In the conclusion to the previous section, I also wrote: “But the lure of mechanism, of the analytic-synthetic approach, is too strong.” It is indeed. Economists have built whole careers on this approach and are not happy to admit to its inappropriateness for social science. And when the financiers built whole Empires of Private Money on top of the economists’ analytic-synthetic approach, the manhandling of complexity turned from bad science into an oppressive regime – one that is now, post-2008, collapsing, with terrible repercussions for almost everyone.
A.3 Economic theory as a form of Motivated Complexity Denial
Economists are smart people. They see that their advice to Ann in the gold sovereign game is pretty poor and realise that they must do better. But they are not prepared to do the decent thing, which is to confess that, in a truly strategic social context, the analytic-synthetic approach is bunk. That this game’s complexity is not amenable to modelling, however clever the modeller. With glorious careers and CVs based on the analytic-synthetic approach and the ‘commercial’ success of their models, they employ copious amounts of intelligent thinking not in order to shine a light on the problem but so as to shore up their method; to restore its authority.
The result is models of increasing complexity which, magnificently, obfuscate more ‘efficiently’ the phenomena they are meant to elucidate. But, and this is their aim, their exceptionally obtuse mathematics put them beyond the reach of most people’s critical judgment. If this reminds you of how the CDOs proved successful, on the basis of their mathematically awful complexity (which stopped most investors from understanding what they were buying), it is because the two cases are very, very similar. As is the way in which the European Financial Stability Facility was structured. But more on these later…
To illustrate this form of sophisticated obfuscation, consider once more the gold sovereign game of the previous section. Ann’s subversive logic overturned the conclusion of the economists’ analytic-synthetic conclusion (that it is uniquely rational to let her greed overtake her senses and thus take two coins at the first stage). So, how did the economists respond? Instead of admitting defeat, they went for a tactical manoeuvre: They admitted that the best strategy may involve taking one coin at a time (at least for a while), as a form of ‘bluff’ that will make the other player more cooperative (i.e. willing to take only one coin for a while) but concentrated their intellectual effort on retaining the monopoly of their analytic-synthetic approach on the narrative of what a rational Ann and a rational Ben ought to be doing at each stage of the game.
More precisely, they start by conceding that, when visiting the table with k coins left on it (where k is considerably more than 3), a rational Ann will take into consideration three probabilities:
- pk = probability assessment by Ben that Ann will choose one coin
- πk = probability assessment by Ben that Ann is motivated by more than greed (e.g. by a sense that it is not right to take two coins and kill the game when there are so many coins awaiting both Ann and Ben to collect)
- qk = probability assessment by Ben that Ann is (i) motivated by greed alone but (ii) she will still choose only one coin at this stage
The idea here is to ‘solve’, at each stage k, for a value of qk, as a function of pk and πk [e.g. qk = f(pk,πk)] What is qk? It is the probability that Ann will ‘bluff’ at stage k or, put differently, the probability that, with k coins left on the table, Ann will take one coin in order to convince Ben that she does not only care about her narrow-minded interest but that she is also concerned about his payout or about not being see as too selfish even when she is entirely selfish. And why do this? So as to have him take one coin too so as to exploit him (by taking two coins at a later stage of the game) before he does the same to her.
Employing highly abstract mathematics, economists then get down to work to compute these bluffing probabilities (qk) as a function of Ann’s (and Ben’s) initial reputation for being greedy and analytic-synthetic in her (his) thinking. The result is a form of convoluted mathematical superstition, rather than a model that has anything of interest to say about the actual behaviour of a rational Ann and a rational Ben. The values of qk thus derived are meaningless, from a practical perspective. All they tell us is with what probability a greedy, instrumental Ann must ‘bluff’ so as to ensure that the model can be solved in terms of… qk. What it does not tell us is what is in Ann’s interest to do under the circumstances (i.e. what qk to choose).
In summary, economists elevate their failure (to come to terms with strategic complexity) to a higher plane of mathematical complexity on which the original complex problem remains just as unsolved as it ever were. The only merit of this theoretical complexity is to confuse the mathematically ill-equipped, to have them think that the economists got to the bottom of the problem (when they have done no such thing). In short, it is a thinly veiled form of intellectual fraud. In reality, it constitutes a form of Complexity Denial which, however, allows them to pretend that the complex problem has been disentangled.
The reason why the economists’ efforts are extremely dangerous, and qualify as a form of toxic theory, is that, on the basis of their false claims (for having dissolved complexity) and the associated formulae [i.e. functions like qk = f(pk,πk)], they build theories which then ‘scientifically’ underpin both catastrophic economic policy (e.g. the macro-econometric estimates of the effects of austerity on growth) and the value of financial instruments (e.g. the infamous value at risk of financial institutions).
Epilogue
The purpose of these posts is to discuss the ways in which economic complexity has been misrepresented, denied and mishandled by economists, financiers and politicians. Part A began by focusing on the problematic application of the analytic-synthetic method to socio-economic interactions. It has claimed that economists have, for a while now, pursued an agenda that denies economic complexity its true nature in order to maximise their own discursive power both in the great Universities and in the corridors of power (both public and corporate). In the next instalments we shall see how the economists’ ultra-complex Complexity Denial has contributed significantly to the policies and institutional design that were responsible for the Crash of 2008 and the eurozone’s inexorable disintegration.
NEXT: The next part in this series, Part B, will be entitled “The political lure of naive models in the era of financialisation”.
Further reading:
- Yanis Varoufakis (2008). ‘Game Theory: Can it unify the social sciences?’, Organisational Studies, 29, 1255-77
- Yanis Varoufakis (2006). ‘Rational Rules of Thumb in Finite Dynamic Games: N-person backward induction with inconsistently aligned beliefs and full rationality’, American Journal of Applied Science, 2 (Special Issue), 57-60
- Shaun Hargreaves-Heap and Yanis Varoufakis (2004). Game Theory: A Critical Text, London and New York: Routledge
- Abstractions and morality in modern finance, Posted by Lisa Pollack on 23rd December 2011, FTAlphaville http://ftalphaville.ft.com/blog/2011/12/23/814381/abstractions-and-morality-in-modern-finance/